Machine Learning — Lagrange multiplier & Dual decomposition

Optimization is a critical step in ML. In this Machine Learning series, we will take a quick look into the optimization problems and then look into two specific optimization methods, namely Lagrange multiplier and dual decomposition. These two methods are very popular in machine learning, reinforcement learning, and the graphical model.
Optimization problem
An optimization problem is generally defined as:

which contains an objective function with optional inequality and equality constraints. The general optimization problem is NP-hard. But many classes of convex optimization problems can be solved in polynomial time. When we join f(x₁) and f(x₂) to form the red line below, if f is a convex function, the red line is always above f for points between them, i.e. yᵢ ≥ f(xᵢ).

A convex optimization problem has its objective function to be convex and its feasible set to be a convex set. A feasible set is the set of x that satisfy the constraints. In a convex set, any value between two points in the set must belong to the convex set also.

From another perspective, in a convex optimization problem, f and l are convex functions,

and the equality constraints are affine functions which have the general form:

As a side note, affine functions are convex. We will need that later.
In ML, the objective function for linear regression is often expressed in the least square errors. Least squares optimization problems are well studied. There are many numerical ways to solve them and they can be solved analytically (normal equations) unless certain scalability limitation is reached. They are relatively easy to solve in optimization.

Otherwise, if the ML problems can be expressed in a linear program, we can apply linear programming. This is also well studied. The feasible set for x in a linear program is a polyhedron.

In our example above, the dotted lines are the contour plot of the objective function. The optimal x* will be one of the vertexes.
In general, if the problem is a convex optimization problem, we can solve it numerically. A function is convex if its second-order derivative is positive for all x.

In ML, we often transform, approximate or relax our problems into one of these easier optimization models.
Lagrange multiplier
Let’s focus on finding a solution for a general optimization problem. Consider the cost function f=x+y with the equality constraint h: x² + y² = 25, the red circle below.

To enforce constraint, we move orthogonally to the normal of the constraint surface, i.e. perpendicular to ∇x h. And to reduce cost, we choose one of the paths along the negative gradient of f. An optimal point is reached when we cannot move further to reduce cost. This happens when ∇h aligns with the gradient of the cost function.

i.e.,

h(x) = 0 also implies -h(x) = 0. The sign of λ subjects to how h is defined. Therfore, λ can be positive, negative or zero.
Next, we define the Lagrangian as

If we take the derivative of the Lagrangian w.r.t. x and λ respectively and set them to be zero, as shown below, we enforce the optimal point described before as well as the equality constraint.

So by finding the optimal point of 𝓛 w.r.t. x and λ, we locate the optimal solution with the equality constraint enforced. We can have multiple constraints and inequality constraints in the Lagrangian also. The optimization problem will be in the form of:

and the Lagrangian is defined as:

Now the inequality constraint requires the optimal point to be in the shaded area (inclusively). The gradient of f and l will have the same direction when the solution is optimal, i.e. αᵢ ≥ 0.

Let’s have another observation regarding the inequality constraint. The left figure below represents a cost function f with the optimal solution be the center of that circle.

In the middle figure, we add an inequality constraint to the optimization problem. But this constraint is redundant because the unconstrained optimal already fulfill this constraint. So αᵢ can simply be zero to indicate that it is redundant.
In the right figure, the unconstrained optimal falls outside of l. We have to increase the cost (the red circle) until it touches l. The corresponding lowest cost will have the constraint l equals 0.
Therefore, αᵢ lⱼ(x) always equals 0.

Example
Let’s maximize f(x, y) = x + y subject to x² + y² = 32.
The Lagrangian is:

To solve the optimization, we set the derivate of 𝓛 w.r.t. x, y, and λ to zero respectively.

By plugin the value back to the equations,

We realize the maximum value for f is 8 with x = y = 4.
Don’t expect the solution is that simple for the general optimization problems. We build a visual model to understand the idea intuitively. But there are quite a few holes to fill.
Lagrangian Duality
In our previous discussion, we are working on a convex optimization problem. So it is time to take the convex assumption away.

Consider the following Lagrangian L. Let’s maximize L w.r.t. α.

Let J(x) be
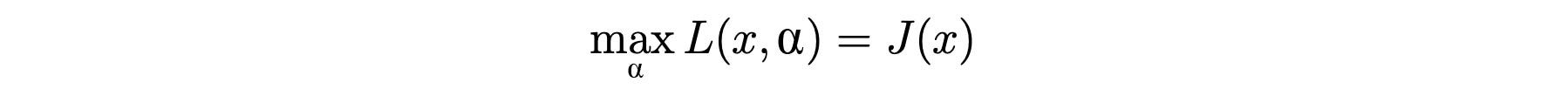
So J will be infinity if the inequality constraint lᵢ(x) ≤ 0 is violated. Otherwise, J is simply f(x). So J is a perfect cost function for our optimization problem that enforcing the inequality constraint. The original objective function becomes

But this is very hard to solve. So let’s view it from a different perspective and discover the relationship between the following minmax solution and the maxmin solution as a possible alternative.

The minmax problem is our original problem and we call it the primal problem. The maxmin problem is called the dual problem.
Let g be

The dual problem maximizes g.

g is a convex function because it is an affine function.

Since g is convex with a linear constraint αᵢ ≥ 0, optimize it is easy. For situations where optimizing L w.r.t. x is easy also,

finding the solution for the dual problem is easy.

However, we come to a big question. Is the primal problem has the same optimal solution as the dual problem?

The general answer is no.

But as shown above, the dual solution d* is the lower bound for the primal solution p* in general if L is smooth. This property is called the weak duality. Maximizing α finds the tightest possible lower bound on p*.

The property that p* = d* is called the strong duality.
Strong duality via Slater’s condition
Strong duality holds when the optimization problem is a convex optimization problem with a feasible x in satisfying the constraints. This is the Slater’s condition, a sufficient condition for the strong duality. There are other sufficient conditions but we will not cover here.
Putting it together
Given a primal problem (the original minimization problem):

We define the Lagrangian as

and the Dual function as

The associated dual problem will be defined as

In general, if L is smooth, the weak duality holds which the dual solution d* will be the lower bound for the primal solution p*, d* ≤ p*. Strong duality holds when d* = p*. It can be achieved through the slater’s condition (necessary condition). The dual problem provides an alternative in solving the primal problem if we can minimize L w.r.t. x easily. The rest will be simple because the result function g will be convex and easy to optimize. If the strong duality condition holds, we are done. If only the weak duality holds, we have a lower bound solution. In some situations, this may be reasonably good as an approximation solution to the primal.
If an optimization problem has a strong duality (for example, it meets the necessary condition like the Slater’s condition), then

KKT conditions
Here are the KKT conditions. If it is true, x*, α* and λ* are the primal and dual solution or vice versa if strong duality holds.

The stationarity condition is where the negative gradient of the cost function f is in the same direction or parallel to the constraint l and h respectively. The primal and the dual feasibility is the conditions required by the corresponding optimization problem. The complementary slackness is a common condition regarding whether the inequality constraints are redundant or not (we cover that already).
Visualization of the Lagrangian multiplier
Let’s visualize our solution. We plot f(x) against l(x) below. The green space spawns all values of x. Our soluting will be one of the points in the green area. The Lagrangian is L = f(x) + α l(x).

In the first step, we fix α. Given α, we can draw a red line to join points of f(x) and l(x) that have the same Lagrangian value. Since α ≥ 0, the line has a negative slope with value -α. The y-intersect (the interest on the f(x) axis) is the value of the corresponding Lagrangian value. In the first step, the dual function g(α) minimizes f(x) + α l(x) over x in the green space above. In other words, we want to have a line with the given slope -α that has the smallest y-intersection providing that it still in contact with the green zone. That is the dotted line on the left above. Since g(α) is a lower bound of p*, the green dot is a lower bound for the optimal value. Our next task is moving up from this point in finding a line with a new slope -α that will barely touch the green space. That is our second step in maximizing g(α). We often find the solution iteratively. We will demonstrate this next.
Dual Gradient Descent
We start with a random guess of λ and use any optimization method to solve the unconstrained objective.

Next, we will apply gradient ascent to update λ in order to maximize g. The gradient of g is:

i.e.

In step 1 below, we find the minimum x based on the current λ value, and then we take a gradient ascent step for g (step 2 and 3).

We alternate between minimizing the Lagrangian 𝓛 with respect to the primal variables (x), and incrementing the Lagrange multiplier λ by its gradient. By repeating the iteration, if the problem is convex, the solution will converge.
Decomposition
Divide-and-conquerer is the best friend of engineers. If a problem can be sub-divided, we can solve an optimization problem as multiple but smaller optimization problems.

However, the formularization above assumes the set of variables in x₁ and x₂ are not overlapping. In many problems, this is not true.

Primal decomposition
But, we can solve the problem in alternating steps iteratively.

If the original problem is convex, the master problem above will also be convex. We repeat the iteration below and apply gradient descent in solving y. In step 1, we minimize f₁ and f₂ accordingly to form 𝜙₁(y) and 𝜙₂(y). We compute their gradients and update y with the gradient descent where α is the learning rate at iteration k.

This algorithm is called the primal decomposition.
Dual decomposition
As expected, if there is a decomposition working on the primal variables of the objective function, there should be a decomposition working on its dual equivalent. In the dual decomposition, we introduce two variables y₁ and y₂ to replace y. But we add a consensus constraint y₁ = y₂, so we are indeed solving the original problem.

The Lagrangian is

where λᵀ is the transpose of λ which is a vector holding the Lagrangian multipliers. The dual problem will be defined as:

The gradient of g₁(λ) and g₂(λ)is simply y₁* and y₂* respectively. Therefore the gradient of g(λ) equals y₂*-y₁*.
The algorithm for the dual decomposition is:

y below can be computed as the mean of y₁ and y₂. Or we can check which value of yᵢ in the later iterations will yield the most optimal solution.

Intuitively, we break down an objective function into smaller sub-problems. We optimize them independently. However, their solutions will not agree. So we add an equality constraint, i.e. the solutions should be the same. Once, we have the constraints added, we solve it with the Lagrangian multiplier. The idea is to find the optimal solutions for each sub-problems while trying to push the solution as close as possible (or equal) to others.
Credits
Lagrange Multipliers and the Karush-Kuhn-Tucker conditions
