
QC — How to build a Quantum Computer with Trapped Ions?
Quantum information processing has been theorized since the 80s but it took a few more decades to develop the first general quantum computer. In 2016, a 5-qubit IBM Q quantum computer was made available to the public via the cloud. Its capability is very limited: it barely factorizes 15 (3×5). Scientists need to optimize the Shor’s algorithm further just to pack the program inside the 5-qubit.

In 2017 and 2018, IBM and Google released a general 50-qubit and a 72-qubit quantum computer respectively. As the number of qubits grows, the potential capacity grows exponentially. We may not be too far from demonstrating the first quantum supremacy. Nevertheless, to commercialize a quantum computer, many scientists believe it needs about a million or more qubits. It is estimated that a 100-million-qubit computer is needed to factor a 2,000-bit number in a day (source). That is the strength of SSL certificates commonly used in key encryption for Internet now. If we break it, we hack the Internet.
Quantum behavior should be everywhere. Indeed, there are no less than a dozen approaches in creating qubits. The following diagram shows some of the most active approaches: including superconducting circuits, trapped ions, nitrogen-vacancy center in diamond, quantum dots, etc…

One may even argue that we can construct a quantum computer using basketballs. But it won’t work. Why is it so hard to build a large-scale quantum computer? As always, the devil is in the detail. Scientist dream is engineer nightmare. In this article, we look into one of the popular approaches — trapped ions. By digging deeper, we know how a quantum computer is built and recognize the requirements and the challenges that we are facing.
DiVincenzo’s criteria
As mentioned before, a basketball quantum computer will not work. It is too hard to manipulate the desired quantum states precisely. So what are the most fundamental requirements for designing a quantum computer? DiVincenzo has listed five major criteria:
- A scalable physical system with well-characterized qubits.
- The ability to initialize the state of the qubits to a simple fiducial state, such as |000…0⟩.
- Long relevant decoherence times, much longer than the gate operation time.
- A “universal” set of quantum gates.
- A qubit-specific measurement capability.
Criteria 1 requires the selection of two quantum states to be used as |0⟩ and |1⟩ — the computational bases of a qubit (qubit detail):

And we can compose qubits to form a composite system, such as

Criteria 2 requires the initialization of qubits to a well-defined state reliably, usually |000…0⟩. Both of these criteria seem simple but it takes the majority of this article to explain the physics.
Criteria 3 addresses the decoherence which is a major problem in quantum computers. Qubit is very delicate. Noise, heat, electromagnetic fluctuation, vibration or particle spin from the surrounding environment or the control line corrupts the information of a qubit. Once you hit the run button, quantum information starts degrading. You cannot pause the program and take a break.
The quality of a quantum computer design is measured by the relaxation time (T1), coherence time (T2), readout errors, and gate errors.

T1 is the time taken for the excited |1⟩ state to decay toward the ground state |0⟩. T2 is the dephasing affects the superposition phase which also includes the effect of energy relaxation.
We often isolate the qubits so the perturbation from the surroundings can be reduced. In the superconducting circuit, we cool down the quantum processor to temperature even lower than the outer deep space. For trapped ions, we isolate the ions in a vacuum chamber. In some unusual cases, isolation comes naturally. For example, the interior of a diamond is a good isolated environment. That makes the nitrogen-vacancy center (N-V center) in diamond appealing to quantum computing.
Criteria 4 requires us to build a set of operations to manipulate the qubits. It is proven that it can be done with a set of universal quantum gates composed of the unitary single-qubit and 2-qubit gates. Ironically, criteria 3 and 4 can be in conflicts. If a qubit cannot be disturbed easily, it may be hard to control. Therefore, long decoherence times often lead to longer gate operation time.
Criteria 5 simply requires us to make measurements precisely. This is quantified by the readout error. Combining this with T1, T2, and the gate errors, it forms the basic metric in evaluating a qubit design. For our basketball quantum computer, it cannot achieve any of these criteria. As shown below, these quantitative performance benchmarks are constantly probed and provided during the operation of a quantum computer.

Next, we look into trapped ion which is heavily studied in the academic and spawn off a few startups in the last few years.
Trapped Ions

Quantum mechanics and atomic physics have been studied together for over a century. Atom is one of the most natural and move-in-ready places for quantum information. Scientists built optical, microwave and laser equipment to manipulate atoms for decades and some of those instruments, like the Caesium fountain atomic clock, are the most accurate instruments we get. Such know-how gives a good start to build a quantum computer. The first decision will be selecting two energy states separately for the computation bases |0⟩ and |1⟩.
Electrons can transit from one energy level to another by absorbing or emitting a photon. In other words, we can use lasers, a coherent source of photons with a specific frequency, to control the energy level of an ion. Since the energy levels are quantized, it is restricted to specific levels as demonstrated below.

When an electron drops to a lower energy state, it releases a photon with a frequency ω corresponding to the difference in energy.

In reverse, to jump to a higher orbit, the electron needs to absorb a photon of the corresponding frequency.

When an atom is at an excited state, it may spontaneously return to one of lower energy state after some time by emitting a photon in a random direction. This is called spontaneous emission. There is another kind of emission called stimulated emission. By shining a photon with energy equals the allowed energy difference, one extra photon will be emitted in the same direction of the incoming photon.

Stimulated emission can be used to control the energy of an atom to another specific level before the spontaneous emission kicks in. In quantum computers, we use both emissions to initialize the state of a qubit.

Let’s have a high-level overview. First, we heat up Calcium to 800°C to form a vapor. We bombard it with electrons to strip out the outer electron. Then, we trap these ions with an electrical field in ultra-high vacuum. We laser-cool these ions to the motional ground state (details later) and use this state as the |0⟩. These ions are now close to stationary. Their states, as well as their motion, can be controlled with high precision using lasers, microwave or radio-frequency fields, which form the foundations of the quantum gates. To measure the qubits’ states, we shine them with another laser with a specific calculated frequency. If the qubit is in one of the states say |1⟩, it will fluoresce else it remains dark.

The diagram below shows how we trap the ions with electrodes (in skin tone color) and control them with the lasers — the two red arrows form a 2-qubit operation. We use a CCD camera to check what ions are shining or not when measured by a laser beam.

Now, let’s get into details. We have selected the laser-cooled motional ground state as |0⟩. So, what is |1⟩? To answer that, we need to learn the energy levels of an ion and its energy transition. The diagram below is the electron configuration of a Calcium atom in different orbits.

After stripping an electron from a Calcium atom, there is only one electron left in the valence shell (the outer shell) and the ground state is 4S. The ion structure will resemble a hydrogen atom (with one electron) which has relatively simple energy levels. Such a simple structure allows us to use fewer lasers to cool the ions down to the ground state and manipulate them without ambiguity. The diagram below illustrates the ground states 4S and its nearest excited states of the Calcium ion. As mentioned before, we pick 4S as |0⟩.

3D and 4P are the nearest excited states respectively and are separated from 4S by optical energy (emitted or absorbed a photon with wavelength inside the visible or near visible range). This diagram also demonstrates the lifetime of the excited states and where it may de-excite to. For instance, the excited 3D (5/2) state of the Calcium ion has a lifetime τ of 1.2 seconds, while the lifetime of the 4P state is only about 7 ns (lifetime is proportional to how quickly it can be de-excited or decay.)
Electric dipole transition v.s. quadrupole transition
To understand these energy transitions, interaction models between an atom and an electromagnetic field are built. But such a model is complex and need further simplification and approximation. For example, the 4P to 4S transition is approximated with an electric dipole approximation, i.e. the transition is contributed by the electric part of the electromagnetic field (ignoring the magnetic part) and the atom behaves like an oscillating electric dipole. Furthermore, selection rules are derived based on this model and the conservation rule of energy, angular momentum, and parity. These rules govern what transitions are allowed or forbidden under this model (or the transition probability).

The transition between 4S to 4P is an allowed electric dipole transition. But it has a short coherence time and therefore a bad candidate for |1⟩. But it is good for preparing the qubit to |0⟩ because of its quick response time.
3D (5/2) to 4S transition is forbidden by the selection rule of the electric dipole transition (a change of 2 unit in orbital length of momentum is not allowed). While it is called forbidden transition, it does not mean it does not happen — we just need a more complex model. Indeed, such a transition is allowed under the electric quadrupole model. But the calculated transition probability per unit time is far much smaller for this type of transition — the transition (or coupling) is weak.

But it can be good news. 3D (5/2) to 4S transition has a longer lifetime — 1.2 seconds. Therefore, 3D (5/2) is a good candidate for |1⟩ with coherence time appropriate enough to complete the target quantum operations (trapped-ion quantum gates are currently operating in a microsecond range). This state is called metastable state with a lifetime in the micro or second range — much longer than the excited states with electric dipole transition.
To fulfill the first DiVincenzo’s criteria, we choose two energy states to represent |0⟩ and |1⟩ separately. We have just demonstrated one set of choice: the ground state 4S as |0⟩ and the metastable state 3D (5/2) as |1⟩. To control the transition, we apply a laser in the optical wavelength. The corresponding qubits are called optical qubits.

Here is the frequency for different types of signals for your reference.

However, other candidates are available. For example, we can use a hyperfine structure. Feynman explains the hyperfine structure of a hydrogen atom as:
The electron can have its spin either “up” or “down,” and the proton can also have its spin either “up” or “down.” There are, therefore, four possible spin states for every dynamical condition of the atom. That is, when people say “the ground state” of hydrogen, they really mean the “four ground states,” and not just the very lowest state. The four spin states do not all have exactly the same energy; there are slight shifts from the energies we would expect with no spins. The shifts are, however, much, much smaller than the 10 electron volts or so from the ground state to the next state above. As a consequence, each dynamical state has its energy split into a set of very close energy levels — the so-called hyperfine splitting.

In short, the spin of the atom nuclei interacts with the spin of the electron and create hyperfine structure. Here is part of the structure for the positive Yb ion.

We can use the split |↑⟩ and |↓⟩ states above as |1⟩ and |0⟩ respectively. This two hyperfine level is chosen because it is insensitive to the magnetic field to some extent. Hyperfine structures are extremely stable and can be treated as ground states. It decays to a lower state with the magnetic dipole transition which is very weak. The superposition formed from these states has coherence in seconds or minutes. We call this hyperfine qubits.
Both types of qubits are easy to measure. And optical qubits with non-zero nuclear spin and some hyperfine levels are insensitive to magnetic fields to a certain extent. This reduces the magnetic impacts from the environment. But all the control signal routing and switching are not easy to implement in addressing individual ions. In addition, driving high-fidelity gates on a long string of ion qubits is hard. This hurts scalability — how many qubits the system has. This is a major challenge in trapped ion computers.
Optical qubits have a shorter lifetime compared with the hyperfine qubit. It requires a narrow linewidth laser, otherwise, dephasing (T2) will be bad. This is not easy.

Hyperfine qubits are extremely long-lived, longer than the optical qubits. It uses lower frequency lasers that are easier to handle and it is widely available commercially and highly accurate. But hyperfine qubits have a narrower energy difference with the presence of other hyperfine neighbors. Initializing and controlling the qubits requires more complex schemes. Because the microwave has a longer wavelength, addressing ions and producing spin-dependent forces precisely is harder. To overcome the problem, we can use Raman transitions (details later). But it takes relatively high-intensity laser light (source). In addition, Raman scattering may occur that can behave like a measurement and the superposition may collapse (source).
Optical and hyperfine qubits are studied by different institutes (even though hyperfine qubit seems more popular). Different tradeoffs (1, 2, 3) show up in the detail implementation.
Choice of ion
The energy level of an atom is uneven. This is important since the laser that excites an electron from |0⟩ to |1⟩ will not mistakenly excite it to an even higher energy state. Because the spacing is uneven, we can drive particular transitions with great simplicity.

Besides Calcium, we do have other choices. The positively charged Calcium ion is well suited for a quantum computer. As mentioned before, it has only a single electron in its valence shell with close resemblance to a hydrogen atom. But, there are other candidates that have similar behavior and mark inside the red rectangles below:

Since the energy levels for each element is different, the photon absorbed or emitted is different too. Hence, the choice of the atom determines the lasers required. This becomes an important design decision. For example, Yb ion with hyperfine qubit is heavily studied even though it is heavier and therefore harder (or require more power) to manipulate. But this qubit can be manipulated with lasers in the microwave range. The laser needed in the implementation is available commercially with great accuracy. Some elements, like Hg, need to deal with deep ultraviolet wavelength. This type of electromagnetic radiation can quickly damage conventional optical fibers. In addition, Yb has a 1/2 spin for the nuclei which make the hyperfine structure (only 4 possible states) simpler than other elements, and therefore easier to manipulate. For this reason, the hyperfine qubits for Yb become a favorite in quantum computers.
Ion Trap & Laser cooling
To manipulate ions, we need them to be as stationary as possible. This is the opposite of how we picture fast moving energetic ions. Fortunately, we can trap ions using electrical fields in ultra-high vacuum (a 100,000-millionths of the normal pressure) and laser-cooled them to extremely low temperatures. i.e. we lower the kinetic energy of the ions to an extremely low level. The ions will float inside the vacuum chamber under an electrical field at a precise location (close to stationary). Once it is done, the ions will have a temperature close to nearly absolute zero even the chamber is operated at room temperature. Before detailing the laser cooling, here is the animation of how it works:
Paul Trap
The short video below is a perfect concept demonstration for Paul Trap used to trap ions.
But instead of using gravitation pull to create the potential well, scientists use electrodes (the rods below) with a high amplitude radio frequency electric field to trap ions. It creates the same potential well described in the video.

Below is an ion trap build on top of a chip so we can reuse the microfabrication know-how to control the ions.


To have a complete picture of the whole system, the diagram below shows the vacuum chambers with the ion trap. One key advantage of trapped ion is that it can operate in room temperature. Unfortunately, an absolute vacuum is not achievable. For some design, to increase the number of trapped ions further, we may cool the system down to reduce the possible collision with the background gas.

Doppler cooling (Laser cooling)
How can we slow down ions? Based on the relativity theory, a laser has momentum even without mass. Watch the next 10 seconds in the video for such experimental proof.
If a laser can move objects, it can stop objects too. We just need a smart way to turn it on and off. So when the ion is moving towards a laser gun, we turn on the laser to slow it down. Otherwise, we turn it off. But how can we do it?

As discussed before, an atom absorbs a photon with specific frequencies only (say a blue laser).

But as the ion move towards the laser beam, according to the Doppler effect, it will be blue shifted. Therefore, we can tune the laser below the target frequency. If the ion move towards the laser, the laser will be blue shifted and absorbed.

Otherwise, it will not be absorbed.

This is our automatic on/off switch. The ion will be slow down when the photon is absorbed. A photon will be emitted by the ion during the spontaneous emission. But since the emission is in a random direction, it has a net zero momentum change in average.

To slow down ions, we just need to place the lasers in different directions.

Doppler cooling is applied to the 4S(1/2) — 4P(1/2) electric dipole transition (397 nm). However, there is about 6% probability of spontaneous decay to the long-lived 3D(3/2) metastate. Therefore, this state is simultaneously pumped out (866 nm) and therefore, the Doppler cooling requires at least two lasers.
Nevertheless, even the net momentum is zero on average over time, the mean squared velocity is non-zero. i.e. the ions still process a certain amount of kinetic energy. With Doppler cooling, we can drop the temperature of the Calcium ion to 0.5 mKelvin. To further reduce the temperature, we need optical pumping.
Optical pumping
Consider we can shine a laser with a specific frequency to excite a lower energy state to a higher energy state plus one more hyperfine step.

Then we let the spontaneous emission to happen. It will fall back to ①, ② or ③.

When they are back in ① or ②, it can be pumped up again by the same laser. But if it lands at ③, it will be stuck because the corresponding pump will not reach a valid energy state and therefore will not happen. In this example, we increase the energy level to the higher hyperfine state. But by carefully selecting the laser, we can lower the energy to the lower hyperfine state instead (this will be demonstrated later).
Resolved-sideband cooling
The trapped ions line up as a string (a crystal string) inside the ion trap. To cool the ion further, we need to include the motion back into the energy model.

Inside the trap, ions are interacting via the Coulomb force like a harmonic oscillator.

It oscillates:

To demonstrate that, here are some of the possible vibrational modes of the trapped ion with each mode carries a different energy level.

In the quantum world, energy is quantized including this harmonic oscillator model, i.e. ions are oscillating in different vibration quantum number. The diagram below includes the vibration quantum number in the corresponding energy levels:

We will tune a laser such that it resonant with a red sideband transition: it excites the ion from |g, n⟩ to|e, n − 1> but with one level drop of the vibration quantum number. The corresponding spontaneous emission followed will have no change in vibration quantum number in average. So the overall process will have a drop of one quantum number in average. So by continuing applying the optical pumping, the ion will eventually reach |g, 0>. But to have a discrete ladder of energies corresponding to different vibrational quantum numbers, the spontaneous decay rate needs to be much smaller than the vibrational oscillation frequency of the ions. This requires a low decay rate for the transition (which may not be available). In Raman sideband cooling, we use two laser beams to provide such transition instead.
Raman Sideband Cooling
The first laser beam excites the atom to a virtual excited state — an intermediate virtual state that is not observable. Then, the second beam de-excites the atom to another hyperfine level. The frequency difference of the two laser beams equals the difference between the two hyperfine levels. The ion loses a vibrational quantum of energy each time a stimulated Raman transition takes place.

To complete the cooling process, another laser is applied to |aux> which indices another spontaneous Raman transitions. If it drops to |1, 0>, it will be stuck otherwise we can perform the optical pumping again.

Recap
The following is the possible workflow of a quantum computer. The first three steps involve laser cooling. The fourth step utilizes the same cooling technique to prepare the ground state |0>. Then we apply quantum gates to manipulate the qubits followed by measurements (read-out).

Here are some of the lasers that may involve

Throughout this article, we will cherry pick technologies just to simplify our discussion. So be warned that there are many other popular approaches and implementations. It is not our scope in giving a comprehensive review. This is a large topic and we suggest readers to do more research on their own if they want details. Understanding the math and the transition model is un-avoidable to learn this subject better.
Measurement — State selective fluorescence detection
To measure the state of the qubit, we use cycling optical transition. We first calculate the frequency that can excite the ion from S to P for either |0> or |1> state. By shining the laser on the ions continuously, the atom will be excited and de-excited through emission. Since we are in the rang of optical transition, a photon in the visible or near visible range is emitted.

But for the same laser, it will not excite the other state that we have not chosen — the photon does not provide the needed energy to excite the atom to a valid energy state.

In our example, the selection rule will allow the excited state to decay to |↑> but not |↓> and therefore the process will repeat itself as we continue shining the lights on the ions. During the whole process, a large number of photons are emitted and part of them will be captured by a CCD camera. In short, ions fluorescence or go dark depends on the state.
Qubit manipulation
The energy gap between the selected hyperfine state is in the microwave range. To be exact, we can shine a 12 GHz microwave on the ion to rotate the qubit and create superposition. However, the relatively long wavelengths limit the spatial resolution. It is harder to address individual ions. In addition, we want to couple the motion with the spin in creating a 2-qubit gate. That requires a higher gradient in the electric field than what the microwave provides. Alternatively, we reuse the Raman transition (mentioned before) to control a qubit with two laser beams. This turns into a two-photon transition that behaves like the previous microwave.

Both lasers are detuned (Δ) far enough from the excited states so there is no direct scattering from the allowed excited states. This will decrease the response time of the quantum gate but can be compensated by increasing the intensity of the laser. But if we increase the intensity too far, scattering may occur and allow us to determine the state of the qubit. i.e. we just perform a measurement and the superposition will collapse (destroy). But usually, if the detuning is far enough, the problem is easy to manage. Another problem that may encounter is the close proximity to other hyperfine levels. We may apply a magnetic field to widen the difference and use polarized lasers to make transitions to the unwanted hyperfine level unlikely (detail). As described, the theory is simple but the details hurt.
CNOT-gate
It can be proven that the all the multiple-qubit gates we need is just the 2-qubit CNOT gate. With other single-qubit gates, it forms a universal set of operations for a quantum computer. The following is the input and expected output for the CNOT-gate. The first qubit is the control qubit. If it is |1>, it flips the second qubit, otherwise, it is unchanged.
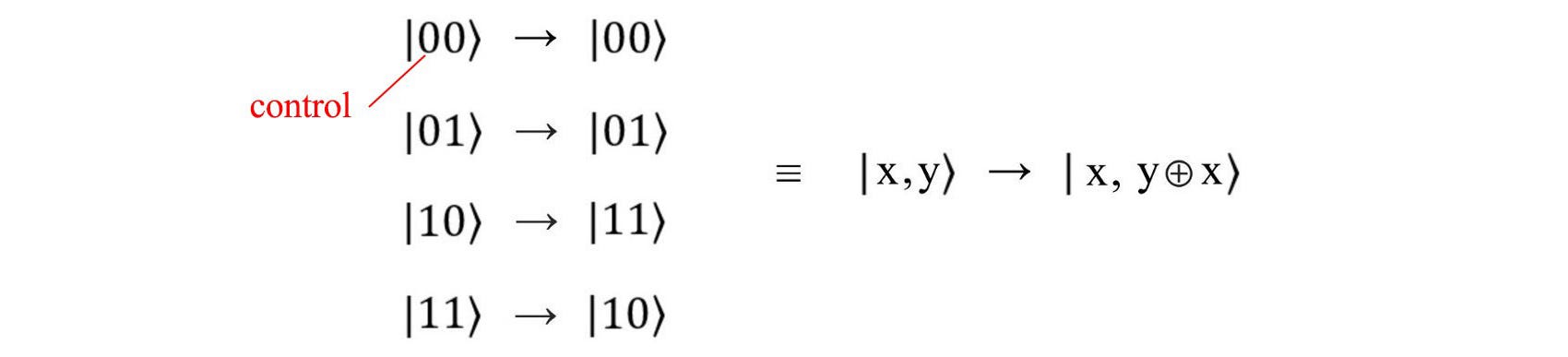
In our previous discussion, we manipulate qubit independently by shining lasers on them. To change the state of the second qubit subject to the first qubit, we need information sharing. How is the state of one qubit is shared with the other qubit?
So far, we learn that there are allowed and forbidden energy transition for an ion. So by shining a laser on an ion, the resulting energy state depends on its state. An ion at one state may make a transition while an ion in another state may not if the transition is forbidden. To implement a 2-qubit gate, information needs to be shared among the qubits. Spin is tied to an atom and not shared with other qubits. But motions in this string of ion are shared and quantized. This motion of ions is shared through the Coulomb force. This will be the secret recipe.

Our final objective is to keep the first qubit unchanged after the operation while the state of the second qubit will depend on the first qubit. First, we shine a laser on ion A with a specific frequency. Ion A will response only if it is in a particular state. In the other state, it will lead to a forbidden state and therefore, it will not happen. But we also shine the ion A with sufficient energy to have the motion of the ion string to jump to a higher quantum vibration mode. Since the vibration mode is shared among ions, that forms the mechanism in sharing information according to the original state of ion A.
Now, we shine ion B a specific laser pulse. The state of the qubit will flip if the string is vibrating in a higher excited state. Now, we are done with the second qubit. The final step requires us to restore the original state of ion A and the string vibration. To accomplish that, we shine a laser of a specific frequency to cancel the vibration of the string and return A to its initial state if it happened. This whole concept works if we know what frequency of the laser is needed to manipulate one state while a transition is forbidden in the other scenario.
The diagram below shows the|↑⟩ and |↓⟩ states with the corresponding vibrational quantum numbers.

Now, we can form a superposition with computational bases |↑⟩, |↓⟩ and the vibrational number. We can design a laser to drive |↑, 0⟩ down to |↓, 1⟩ but the same laser will not make any transition for |↓, 0⟩ because there is no |↑, -1⟩. So we start with the superposition of the first ion below:

And this string of ion is in the motional state [0] (L.H.S. below).

We apply a laser to map the spin information into motion information (vibrational quantum number) as described before. |↑, 0⟩ state is mapped to |↓, 1⟩ while a|↓, 0⟩ remains unchanged.
The spin becomes definitely down for the first ion with new motional state shared among the ions. Then a second laser is applied designed to flip the spin depending on the state of the motion. Finally, we apply a laser to the first ion again to restore it back to the original state. i.e. convert the motional information back to the spin. These combined steps form the entanglements we want.
This concept is proposed by Cirac and Zoller and other alternative concepts are also introduced later. In another approach, we shine lasers on the ions. It moves the ions up or down depending on the state of the spin. Without going into details, it maps the input state non-linearly below. That forms the entanglement we want.

Implementations
The following are the realization of the trapped ion quantum computer. It has a global beam (Global Raman beam) to control all the ions. The hard part is to address individual beams by AOM with all the necessary switching and routing. On the top, it uses the PMT to perform the measurement.

There is a key advantage of using a laser to create entanglement. There are less or no restriction or which two qubits can be connected to form a 2-qubit gate. Such luxury is not available to many other quantum computer designs. But as the number of trapped ions increases, it forms a large string of ions that is susceptible to noise and coherence becomes a problem. To address that, scientists break up the system into modules with each module trapping a limited amount of ions. For example, different strings of ions can be trapped in different regions.

To facilitate communication between modules, we apply methods to transfer an ion from one module to another. But this is still in early research and we will not detail further.

Some thoughts
This article actually introduces a general theme of the quantum computer design. We understand different energy levels of the underneath quantum systems (natural or artificial) and its energy transition rules. We pick two levels that are relatively stable with longer coherence time and with transition rules that make the qubit easier to initialize and to manipulate without ambiguity.
Ions are move-in storage for quantum information. But it is not specifically designed as a computer, a lot of physics is needed to prepare and to manipulate them. Alternatively, we can create an artificial quantum system. But those systems so far is at the macroscopic level which is vulnerable to the environment or masks out easily. It often has a shorter coherence time even its design is more tailored to what we want.
This article presents an overview picture of what is happening. Hope it moves readers one step closer to understand its challenges and potentials. This is the last of this Quantum Computing series. It is a slight detour from what I mainly do professionally but hopes you will enjoy it. For those people interested in this series, here is the link for your reference.
Further readings
Implementing a strand of a scalable fault-tolerant quantum computing fabric
Quantum Computing and Simulation with Trapped Ions
Hyperfine Coherence in the Presence of Spontaneous Photon Scattering
