QC — Phase estimation in Shor’s Algorithm
Phase estimation is an abstract concept but a crucial part of period finding in Shor’s Algorithm. We use it to solve a typical linear algebra problem — given a matrix and its eigenvector, find its eigenvalue. This concept seems unrelated to period finding. But it turns out we can reformulate the problem such that the eigenvalue is related to the period. Finding the eigenvalue leads us to the period of a function. In fact, phase estimation is important to many other quantum algorithms. So let’s explore it in more details. If you want to go back to the last part of the Shor’s algorithm series, here is the link to the Quantum Fourier Transform.
Eigenvalue & Eigenvectors
The eigenvalue and the eigenvector of a matrix A satisfy the following relationship.

Phase estimation is about finding the eigenvalue of a unitary operator. Since a unitary operation preserves the norm of the state vector to 1, the corresponding eigenvalue is just an exponential complex function with real value ϕ below. ϕ is between 0 and 1 (we will use that later). Phase estimation simply means estimate the value of ϕ in the eigenvalue.

In Shor’s algorithm, we want to find the period of some modulo function.

But to do it efficiently, we establish a relationship between the period of a function and the phase value of the eigenvalue. So solving the phase helps us to find the period.

It will take a while to establish this relationship. So, we will focus on phase estimation for now.
Phase estimation
If we know U and |ψ⟩ below, we can estimate ϕ.

One way to do it is to use a controlled-U gate below with the eigenvector |ψ⟩as the input to the target bits.

The expected measurement for the control bit above will be:

Therefore, by repeating the calculations many times, we can use the measurements to estimate ϕ. However, to compute this value with an accuracy up to m bits, the number of re-calculations is in the order of

This is bad because we bring back the exponential complexity again. To reduce the number of measurements, the circuit is redesigned to:

For each step, the operator below is the square of the previous one. This sounds complicated and turns out to be simple for modulo arithmetics. But we will wait until the next article to discuss the implementation.

We use the eigenvector as the input to the target bits (note, we change our previous notation from |ψ⟩ to |u⟩ here). As mentioned before, ϕ is between 0 to 1. Therefore, we can represent it with:

(e.g. ϕ = 0.10111…) We can rewrite the lowest bit for the control as:

(The reasoning is already discussed here)
Since

(In our example, this becomes 1.0111…) and we apply

Therefore, the second lowest bit can be simplified to:

i.e. we just left shift ϕ and remove the integer part since we can ignore any integral multiplication with 2π. So the circuit above just prepare the following supposition:

or

Recall previously that, Quantum Fourier Transform can be implemented as:

So, our prepared superposition is just the inverse QFT of the phase.

So by applying the inverse of the QFT on the prepared superposition, we can find the phase value. As shown below, the left side circuit prepares the superposition and the right side apply the inverse of QFT.
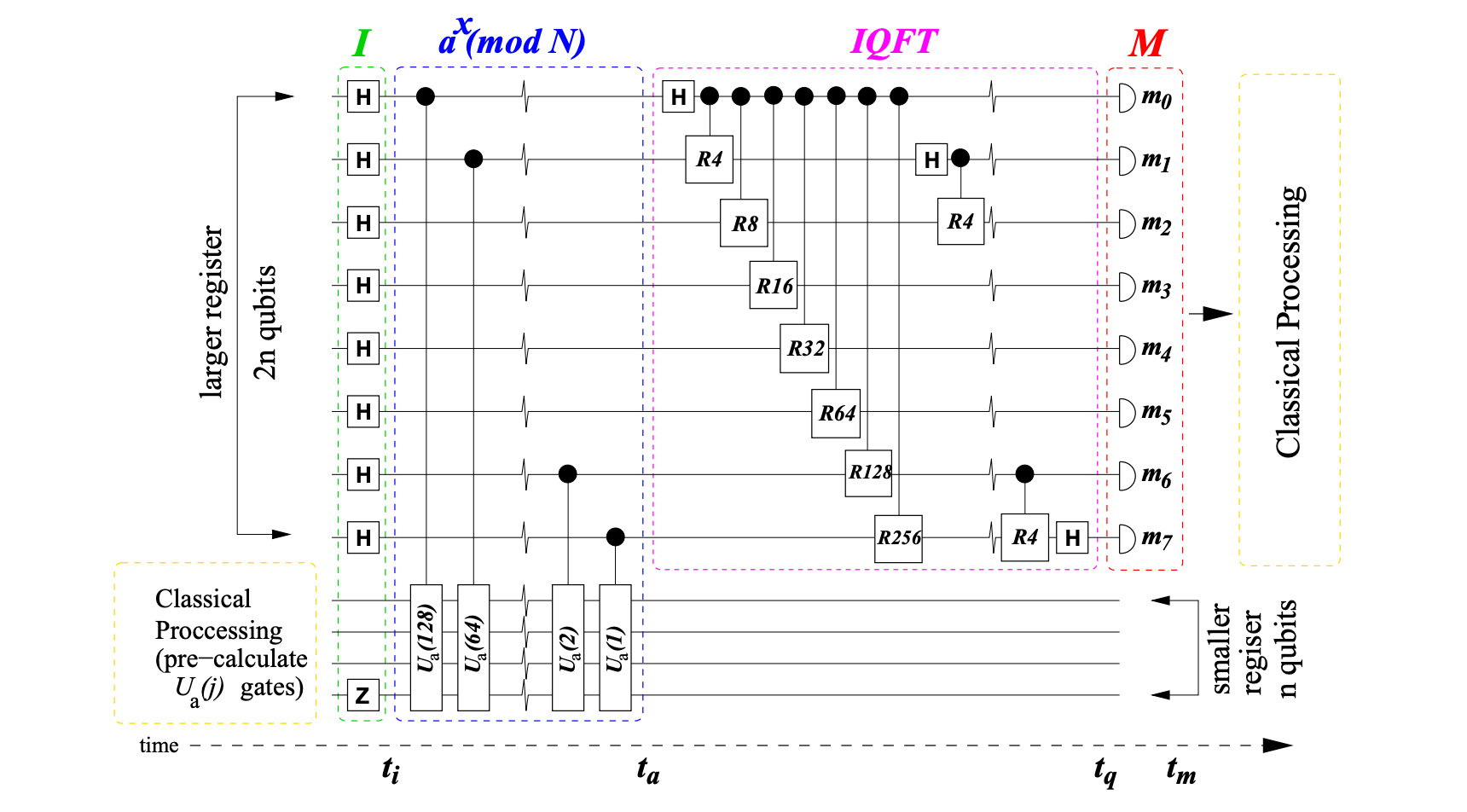
To achieve accuracy to m bits with the probability at least (1 − ε), we need t qubits for the controls:

We will use this information later to find out the number of qubits we need to estimate the phase. For |u⟩, we need enough bits to represent the eigenvector. Since the function mod N has a maximum value of N-1, we just need enough bits to represent N-1.
Recap
Here is the general circuit design for phase estimation.

The first phase includes preparing a superposition with the eigenvector |u⟩ and then apply inverse Quantum Fourier Transform.

Here is the general summary:

Next
This is a long journey. Next, we will put everything together and solve the prime factorization finally.
