Monte Carlo Tree Search (MCTS) in AlphaGo Zero

In a Go game, AlphaGo Zero uses MC Tree Search to build a local policy to sample the next move.

MCTS searches for possible moves and records the results in a search tree. As more searches are performed, the tree grows larger as well as its information. To make a move in Alpha-Go Zero, 1,600 searches will be computed. Then a local policy is constructed. Finally, we sample from this policy to make the next move.

MCTS Basic

In this example, the current board position is s₃.

In MCTS, a node represents a board position and an edge represents a move.

And for a given position, we can compute:

• the policy p (p is a probability distribution scoring each action), and
• the value function v (how likely to win at a board position).

using a deep network f.

In the example below, it applies a deep network f, composed of convolutional layers, on s₃’ to compute the policy p, and the value function v.

We can expand the search tree by simulating a move. This adds the corresponding move as an edge and the new board position as a node to the search tree.

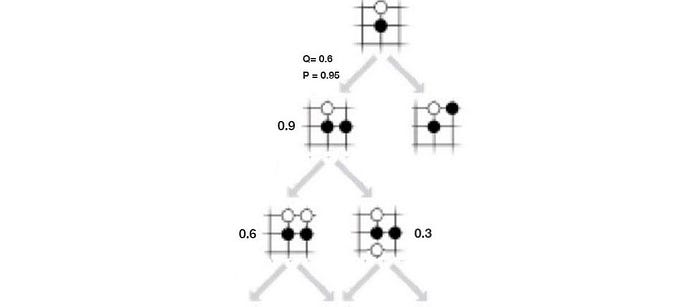
Let’s introduce another term called action-value function Q. It measures the value of making a move given a state. In (a) below, it takes the move in red and f predicts a 0.9 chance of winning. So Q is 0.9. In (b), it makes one more move and ends up with a 0.6 chance of winning. Now, the move a₃ is visited twice, so we set the visit count N=2. The Q value is simply the average of previous results, .i.e. W=(0.9+0.6), Q = W/2=0.75. In (c), it explores another path. Now, a₃ is visited 3 times and the Q value is (0.9+0.6+0.3)/3 = 0.6.

In MCTS, we build up a search tree gradually using s₃ as the root. We add one node at a time and eventually after 1.6K searches, we use the tree to build a local policy (π₃) for the next move. But the search space for Go is huge, we need to prioritize which node to add and to search first.

There are two factors needed to consider: exploitation and exploration.

• exploitation: perform more searches that look promising (i.e. high Q value).
• exploration: perform searches that we know less (i.e. low visit count N).

Mathematically, it selects the move a according to:

Q controls the exploitation and u, an exploration bonus, controls the exploration.

For state-action pairs that are visited frequently or less likely to happen, we have less incentive to explore it more. Starting from the root, it uses this tree policy to select the path that it wants to search next.

In the beginning, MCTS will focus more on exploration but as the iterations increase, most searches are exploitation and Q is getting more accurate.

AlphaGo Zero iterates the steps above 1,600 times to expand the tree.

Surprisingly, it does not use Q to build the local policy π₃. Instead, π₃ is derived from the visit count N.

After the initial iterations, moves with higher Q value will be visited more frequently. It uses the visit count to calculate the policy because it is less prone to outliners. τ is a temperature controlling the level of exploration. When τ is 1, it selects moves based on the visit count. When τ → 0, only the move with the highest count will be picked. So τ =1 allows exploration while τ → 0 does not.

With a board position s, MCTS calculates a more accurate policy π to decide the next move.

MCTS improves the policy evaluation, and it uses the new evaluation to improve the policy (policy improvement). Then it re-applies the policy to evaluate the policy again. These repeated iterations of policy evaluation and policy improvement are called policy iteration in RL. After self-playing many games, both policy evaluation and policy improvement will be optimized to a point that it can beat the masters. Please refer to this article for details, in particular on how f is trained.

MCTS

Before going into the details, here are the 4 major steps in MCTS. As shown, we will start with the board position s₃.

• Step (a) selects a path (a sequence of moves) that it wants to search further. Starting from the root node, it searches for the next action that has the highest value in combing the Q-value (Q =W/N) and an exploration bonus adversely related to the visit count N. The search continues until reaching an action that has no node attached.

• Step (b) expands the search tree by adding the state (node) associated with the last action in the path. We add new edges for actions associated with the new node and record p, computed by f, for each edge.
• Step (c) updates the current path backward on W and N.

After repeating steps (a) to (c) 1,600 times, we use the visit count N to create a new policy π₃. We sample from this policy to determine the next move for s₃.

Next, we will detail each step.

Select

The first step is to select a path from the tree for further search. Let’s assume our search tree looks like the one below.

It starts from the root and we select moves based on the equation below:

where u controls exploration. It depends on N the visit count, P(s, a) the policy from f on how likely we pick a for state s, and c a hyperparameter controlling the level of exploration. Intuitively, the less often an edge is explored, the less information we gain and therefore the higher bonus for us to explore it. Q controls exploitation which is the calculated Q-value function (W/N).

Expand and evaluate

With the selected path decided, a leaf node is added to the search tree for the corresponding action. It uses the deep network f to compute the policy p and v from the added node.

Then for each possible action on the new node, we add a new edge (s, a). We initialize each edge with the visit count N, W, and Q to 0. And we record the corresponding v and p.

Backup

Once p and v are calculated for the leaf node, we backup v to update the action value Q for every edge (s, a) in the selected path.

Play

To decide the next move, AlphaGo Zero creates a new local policy (π₃) based on the visit count for each child of s₃. Then it samples from this policy for the next move.

The selected move a becomes the root of the search tree with all its children preserved while others are discarded. Then it repeats MCTS again for the next move.